Contents

Dictionaries and Sets

Motivation for associative container

The following code simulates the outcomes from rolling a dice multiple times.

dice_rolls = [random.randint(1, 6) for i in range(10)]
print(*dice_rolls)

1 4 2 5 4 5 3 3 6 4

What is the distribution, i.e., fractional counts?

distribution = [dice_rolls.count(i) / len(dice_rolls) for i in range(7)]
plt.stem(range(7), distribution)
plt.xlabel("Outcomes")
plt.title("Distribution")
plt.ylim(0, 1)

(0.0, 1.0)
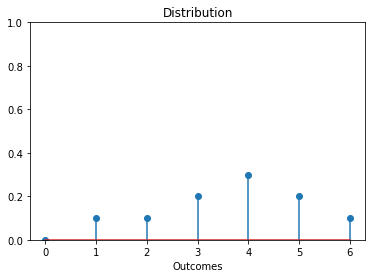
../_images/Dictionaries and Sets_7_1.png

In the above code, distribution[i] stores the fractional count of outcome i.

However, distribution[0] is 0 because a dice does not have outcome 0. Can we avoid such redundancy?

distinct_outcomes = [
    outcome for outcome in range(1, 7) if dice_rolls.count(outcome) > 0
]
distribution = [
    dice_rolls.count(distinct_outcomes[i]) / len(dice_rolls)
    for i in range(len(distinct_outcomes))
]

plt.stem(distinct_outcomes, distribution)
plt.xlabel("Outcomes")
plt.title("Distribution")
plt.ylim(0, 1)

(0.0, 1.0)
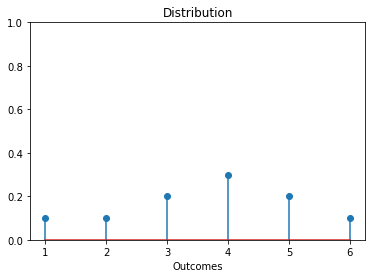
../_images/Dictionaries and Sets_10_1.png

In the above code,

  • distinct_outcomes stores the list of distinct outcomes, and

  • distribution[distinct_outcomes[i]] stores the fractional count of the i-th distinct outcome.

What about finding the distribution of characters in an article?
There are 1,112,064 unicode characters. Can we:

  • Obtain the distribution efficiently without creating an entry for each unicode character?

  • Compute the set of distinct characters efficiently without iterating over the set of all unicode characters?

  • Access the fractional count of a particular character efficiently without searching through the list of distinct outcomes?

  • Index distribution directly by the distinct characters in the article?

What we need is a composite data type that

  • can keep a set of unique keys of different types (such as the characters in our example), and

  • associate to different keys possibly different values of any types (such as the fractional counts of the characters).

Such a data structure is called an associative container.

How to use associative containers in Python?

There are two built-in classes for associative containers:

  • set can store a set of unique keys of possibly different types.

  • dictionary can store a set of key-value pairs.

We have already used sets and dictionaries before.

%%mytutor -h 400
a = (lambda **kwargs: kwargs)(start=0, stop=5, step=1)
b = set([1, 1, 2, 3, 3, 3])
assert len(a) == len(b)

Both set and dict

  • implement len method that returns the number of keys, and

  • are mutable, so we can add/remove keys and values and modify their object references.

Constructing associative containers

How to create set/dictionary?

Similar to tuple/list, we can use enclosure, constructors, and comprehension.

How to create a set/dict by enumerating its keys/values?

For dict, enclose a comma-separated sequence of key : value pairs by braces { and }.

%%mytutor -h 350
empty_dictionary = {}
a = {"a": 0, "b": 1}
b = {**a, "c": 0, "d": 1}

For set, omit : value.

%%mytutor -h 300
a = {(1, 2.0), print, *range(2), *"23"}
empty_set = {*()}  # Why not use {}?

We can also create a set/dictionary from other objects using their constructors set/dict.

%%mytutor -h 550
empty_set = set()
string2set = set("abc")
range2set = set(range(2))
list2set = set(["abc", range(2)])
set2set = set(list2set)

%%mytutor -h 650
empty_dict = dict()
enumerate2dict = dict(enumerate("abc"))
zip2dict = dict(zip("abc", "123"))
kwargs2dict = dict(one=1, two=2)
dict2dict = dict(kwargs2dict)

Exercise dict also has a class method fromkeys to construct a dictionary with keys from iterable pointing to a default value. Create a dictionary using fromkeys with keys being the non-negative integers smaller than 100 and values being 0.

Hint: Use dict.fromkeys since a class method is bound to the class rather than an object of the class.

dict.fromkeys?
### BEGIN SOLUTION
fromkeys_dict = dict.fromkeys(range(100), 0)
### END SOLUTION

# test
assert all(fromkeys_dict[k] == 0 for k in fromkeys_dict)

How to use a rule to construct a set/dictionary?

The following function uses a one-line dictionary comprehension to return the distribution of items in a sequence:

def distribute(seq):
    return {k: seq.count(k) / len(seq) for k in set(seq)}

def plot_distribution(seq):
    dist = distribute(seq)
    plt.stem(
        dist.keys(),  # set-like view of the keys
        dist.values(),  # view of the values
    )
    plt.xlabel("Items")
    plt.title("Distribution")
    plt.ylim(0, 1)


plot_distribution("What is the distribution of different characters?")
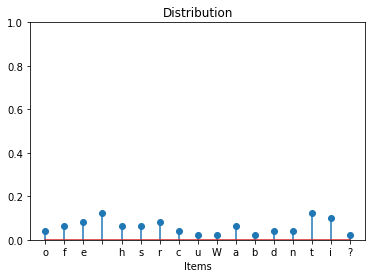
../_images/Dictionaries and Sets_35_0.png

  • The object methods keys and values provide a dynamic view of the keys.

  • Unlike a copy, subsequent changes to the dictionary are also reflected in a previously returned view.

  • items provides a set-like view of the key-value pairs.

%%mytutor -h 500
a = dict(enumerate("abc"))
views = a.keys(), a.values(), a.items()
print(a.pop(1))  # remove the key 1 and its associated value
print(a.popitem())  # remove and return one key-value pair
a.clear()  # clear the dictionary

set has pop and clear but not popitem. However, set.pop behaves like dict.popitem instead of dict.pop.

%%mytutor -h 250
a = set("abc")
print(a.pop())  # remove and return an element
a.clear()  # clear the set

Exercise Use one-line comprehension to return a set of composite numbers smaller than stop.

Hint: You do not need to worry about duplicate elements for set.

def composite_set(stop):
    ### BEGIN SOLUTION
    return {x for factor in range(2, stop) for x in range(factor * 2, stop, factor)}
    ### END SOLUTION


print(*sorted(composite_set(100)))

4 6 8 9 10 12 14 15 16 18 20 21 22 24 25 26 27 28 30 32 33 34 35 36 38 39 40 42 44 45 46 48 49 50 51 52 54 55 56 57 58 60 62 63 64 65 66 68 69 70 72 74 75 76 77 78 80 81 82 84 85 86 87 88 90 91 92 93 94 95 96 98 99

Hashability

For set and dict,

  • identical keys are merged to the same entry even though

  • values associated with different keys can be the same.

%%mytutor -h 350
a = {0: "a", 0.0: "b", 2: "b"}
b = {0j, 0, 0.0, "", False}
assert 0 == 0.0 == 0j == False != ""

This is implemented efficiently by hashing. A key must be a hashable object which:

  • has a hash value (returned by __hash__ method) that never changes during its lifetime, and

  • can be compared (using __eq__ method) to other objects.
    Hashable objects which compare equal must have the same hash value.

def hashable(obj):
    try:
        hash(obj)
    except Exception:
        return False
    return True


for i in 0, 0.0, 0j, "", False, (), [], {}, set(), frozenset(), ([],):
    if hashable(i):
        print("{} may be hashable. E.g., hash({!r}) == {}".format(type(i), i, hash(i)))
    else:
        print("{} may not be hashable.".format(type(i)))

<class 'int'> may be hashable. E.g., hash(0) == 0
<class 'float'> may be hashable. E.g., hash(0.0) == 0
<class 'complex'> may be hashable. E.g., hash(0j) == 0
<class 'str'> may be hashable. E.g., hash('') == 0
<class 'bool'> may be hashable. E.g., hash(False) == 0
<class 'tuple'> may be hashable. E.g., hash(()) == 5740354900026072187
<class 'list'> may not be hashable.
<class 'dict'> may not be hashable.
<class 'set'> may not be hashable.
<class 'frozenset'> may be hashable. E.g., hash(frozenset()) == 133146708735736
<class 'tuple'> may not be hashable.

Why the key should be hashable?
What is the use of a hash value?

Associative containers are implemented as hash tables for efficient lookup of key values.

%%html
<iframe width="800" height="450" src="https://www.youtube.com/embed/LPzN8jgbnvA" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>

Most mutable objects are not hashable. Why?
Mutating a key makes it a different key, which is hard to track.

set has an immutable counterpart called frozenset, but dict does not have any immutable counterpart. Why?
While elements of a set must be hashable and therefore mostly immutable, dictionary values may be of mutable types.

Python also uses dictionary for its global/local frames.
Indeed, hash collisions can slow down the lookup process.

Exercise Why equal objects must have the same hash but different objects may have the same hash? An example is given below:

assert hash(0) == hash(0.0) == hash(0j) == hash(False) == hash("") and False != ""

  1. To avoid duplicate keys occupying different entries in a hash table.

  2. Hash collision can be detected by == and handled by collision resolution techniques. To keep the hash table small, hash collision is unavoidable.

Exercise Should an immutable object always be hashable?

No. hashable(([],)) returns False in particular because the value of an immutable object can still be changed if it points to a mutable object.

Exercise Can we use the id of an object as its hash value?

No because id remains unchanged even if the value of an object changes.

Accessing keys/values

How to traverse a set/dictionary?

Set and dictionaries are iterable.
The for loop iterates over the keys.

a = set("abcde")
b = dict(enumerate("abcde"))
print(*(element for element in a))
print(*((key, b[key]) for key in b))
a[0]  # TypeError

e c a b d
(0, 'a') (1, 'b') (2, 'c') (3, 'd') (4, 'e')

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
<ipython-input-20-66b1bb24cf73> in <module>
      3 print(*(element for element in a))
      4 print(*((key, b[key]) for key in b))
----> 5 a[0]  # TypeError

TypeError: 'set' object is not subscriptable

  • For the dictionary b, we used subscription b[key] to access the value associated with key.

  • Unlike dictionary, set does not implement __getitem__ and is therefore not subscriptable.

Unlike tuple/list, b[-1] does not refer to the value of the last entry. (Dictionary is not ordered.)

b[-1]  # KeyError

---------------------------------------------------------------------------
KeyError                                  Traceback (most recent call last)
<ipython-input-21-784624678be8> in <module>
----> 1 b[-1]  # KeyError

KeyError: -1

The above raises a key error because -1 is not a key in the dictionary b.

Dictionary implements the __setitem__ method so we can enter a key value pair to a dictionary using the assignment operator.

b[-1] = "f"
b[-1]

'f'

To delete a key, we can use the function del.

del b[-1]
b[-1]

---------------------------------------------------------------------------
KeyError                                  Traceback (most recent call last)
<ipython-input-23-a57f788767eb> in <module>
      1 del b[-1]
----> 2 b[-1]

KeyError: -1

To avoid key error, we can check if a key is in a dictionary efficiently (due to hashing) using the in operator.
The following is a different implementation of distribute.

def distribute(seq):
    dist = {}
    for i in seq:
        dist[i] = (dist[i] if i in dist else 0) + 1 / len(seq)
    return dist


plot_distribution("What is the distribution of different characters?")
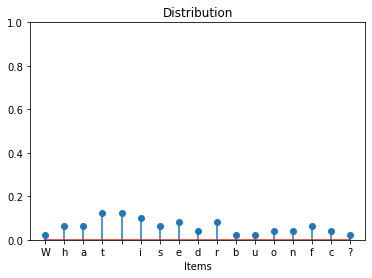
../_images/Dictionaries and Sets_73_0.png

Exercise Unlike the previous implementation using one-line dictionary comprehension, the above alternative implementation uses multiple lines of code to build the dictionary incrementally starting from an empty dictionary.

def distribute(seq):
    return {k : seq.count(k)/len(seq) for k in set(seq)}

Explain whether the alternative is more efficient.

It is more efficient because

  • the alternative implementation traverses seq once with near constant time lookup of the key, but

  • the list comprehension can traverse seq a multiple times linear in len(seq), since every call to seq.count has to traverse seq once.

Shorter code needs not be more efficient.

Exercise dict also has a getter method get that conveniently returns a default value if the key does not exist. Rewrite the alternative implementation of distribute to use get instead of in.

dict.get?
def distribute(seq):
    dist = {}
    for i in seq:
        ### BEGIN SOLUTION
        dist[i] = dist.get(i, 0) + 1 / len(seq)
        ### END SOLUTION
    return dist


plot_distribution("What is the distribution of different characters?")
../_images/Dictionaries and Sets_77_0.png

How to traverse in ascending order of the keys?

We can apply the function sorted to a set/dictionary to return a sorted list of the keys.

%%mytutor -h 600
a = set(reversed("abcde"))
b = dict(reversed([*enumerate("abcde")]))
sorted_elements = sorted(a)
sorted_keys = sorted(b)

Exercise Re-implement plot_distribution to plot the distribution in ascending order of the keys.

Hint: Use the optional argument key of the function sorted.

def plot_distribution(seq):
    dist = distribute(seq)
    # plt.stem(dist.keys(), dist.values())
    ### BEGIN SOLUTION
    dist_list = sorted(dist.items(), key=lambda p: p[0])
    plt.stem(
        [p[0] for p in dist_list], [p[1] for p in dist_list]
    )
    ### END SOLUTION
    plt.xlabel("Items")
    plt.title("Distribution")
    plt.ylim(0, 1)


plot_distribution("What is the distribution of different characters?")
../_images/Dictionaries and Sets_82_0.png

How to add an element to a set and remove an element from it?

Instead of subscription, set has the add/discard/remove methods for adding/removing elements.

%%mytutor -h 400
a = set("abc")
a.add("d")
a.discard("a")
a.remove("b")
a.clear()
a.discard("a")  # no error
a.remove("b")  # KeyError

Other operators and methods

Unlike str/tuple/list, set and dict do not implement addition + and multiplication *:

any(
    hasattr(container, attr)
    for attr in ("__add__", "__mult__")
    for container in (dict, set, frozenset)
)

False

Exercise Use the unpacking operators * and ** to concatenate two sets/dictionaries below into a new set/dictionary.

set1 = set("abc")
set2 = set("cde")
### BEGIN SOLUTION
concatenated_set = {*set1, *set2}
### END SOLUTION
concatenated_set

{'a', 'b', 'c', 'd', 'e'}

dict1 = dict(enumerate("abc"))
dict2 = dict(enumerate("def", start=2))
### BEGIN SOLUTION
concatenated_dict = {**dict1, **dict2}
### END SOLUTION
concatenated_dict

{0: 'a', 1: 'b', 2: 'd', 3: 'e', 4: 'f'}

set overloads many other operators:

%%mytutor -h 550
a, b = {1, 2}, {2, 3}

union = a | b
assert all(i in union for i in a) and all(i in union for i in b)

intersection = a & b
assert all(i in a and i in b for i in intersection)

assert intersection <= a <= union  # subset
assert union > b > intersection  # proper superset
assert len(a) + len(b) == len(intersection) + len(union)

symmetric_difference = a ^ b
assert all((i in a or i in b) and not (i in a and i in b) for i in symmetric_difference)
assert symmetric_difference == union - intersection
assert set.isdisjoint(intersection, symmetric_difference)
assert len(union) == len(intersection) + len(symmetric_difference)

The following uses & and - to compare the sets of public attributes for set and dict:

set_attributes = {attr for attr in dir(set) if attr[0] != "_"}
dict_attributes = {attr for attr in dir(dict) if attr[0] != "_"}
print("Common attributes:", ", ".join(set_attributes & dict_attributes))
print("dict-specific attributes:", ", ".join(dict_attributes - set_attributes))
print("set-specific attributes:", ", ".join(set_attributes - dict_attributes))

Common attributes: pop, update, copy, clear
dict-specific attributes: get, setdefault, values, keys, fromkeys, items, popitem
set-specific attributes: remove, difference_update, add, isdisjoint, issubset, intersection, intersection_update, discard, symmetric_difference_update, issuperset, symmetric_difference, difference, union

For set, the intersection operation & can also be performed by

  • the class method intersection which returns the intersection of its arguments, and

  • the object method intersection_update which mutates a set object by intersecting the set with the arguments.

%%mytutor -h 300
a = {0, 1, 2}
b = {1, 2, 3}
c = set.intersection(a, b, {2, 3, 4})
a.intersection_update(b, c)

  • All other set-specific methods have an associated operator except isdisjoint as shown below.

  • The object method for union is update not union_update.

class method

object method

operator

union

update

\|

intersection

intersection_update

&

symmetric_difference

symmetric_difference_update

^

issubset

<=

issuperset

>=

isdisjoint

dict also has an update method that can update a dictionary using dictionary, iterables and keyword arguments:

%%mytutor -h 300
a = {}
a.update(enumerate("a"), b=2)
b = a.copy()
a.update(b, c=3)

Exercise For dict, there is also a method called setdefault. Use it to define a function group_by_type that

  • takes a sequence seq of objects and

  • returns a dictionary d such that d[repr(t)] returns the list of objects in seq of type t

If there is no objects of type t, raise a key error.

def group_by_type(seq):
    group = {}
    for i in seq:
        ### BEGIN SOLUTION
        group.setdefault(repr(type(i)), []).append(i)
        ### END SOLUTION
    return group


group_by_type(
    [
        *range(3),
        *"abc",
        *[i / 2 for i in range(3)],
        *[(i,) for i in range(3)],
        *[[i] for i in range(3)],
        *[{i} for i in range(3)],
        *[{i: i} for i in range(3)],
        print,
        hash,
        int,
        str,
        float,
        set,
        dict,
        (i for i in range(10)),
        enumerate("abc"),
        range(3),
        zip(),
        set.add,
        dict.copy,
    ]
)

{"<class 'int'>": [0, 1, 2],
 "<class 'str'>": ['a', 'b', 'c'],
 "<class 'float'>": [0.0, 0.5, 1.0],
 "<class 'tuple'>": [(0,), (1,), (2,)],
 "<class 'list'>": [[0], [1], [2]],
 "<class 'set'>": [{0}, {1}, {2}],
 "<class 'dict'>": [{0: 0}, {1: 1}, {2: 2}],
 "<class 'builtin_function_or_method'>": [<function print>,
  <function hash(obj, /)>],
 "<class 'type'>": [int, str, float, set, dict],
 "<class 'generator'>": [<generator object <genexpr> at 0x7f922e36e900>],
 "<class 'enumerate'>": [<enumerate at 0x7f922e38c700>],
 "<class 'range'>": [range(0, 3)],
 "<class 'zip'>": [<zip at 0x7f922e38ca80>],
 "<class 'method_descriptor'>": [<method 'add' of 'set' objects>,
  <method 'copy' of 'dict' objects>]}