CS1302 Introduction to Computer Programming
Run the following to load additional tools required for this lab.
In particular, the math library provides many useful mathematical functions and constants.
import math
from math import cos, exp, log, pi, sin, tan
import jsxgraphs
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
from ipywidgets import interact
%matplotlib widgetThe following code is a Python one-liner that creates a calculator.
Evaluate the cell with Ctrl+Enter:
print(eval(input()))Try some calculations below using this calculator:
- by entering
2**3; - by entering
2/3; - by entering
3//2; - by entering
3%2; - by entering
2**0.5; and - by entering
sin(pi/6);
For this lab, you will create different calculators. We will first show you a demo. Then, it will be your turn to create the calculators.
Hypotenuse Calculator¶
You can verify the theorem using the JSXGraph app below:
jsxgraphs.pythagorean1The following is an interactive graphical proof:
jsxgraphs.pythagorean2Another interactive proof is as follows:
jsxgraphs.pythagorean3We can define the following function to calculate the length c of the hypotenuse when given the lengths a and b of the other sides:
def length_of_hypotenuse(a, b):
c = (a**2 + b**2) ** (0.5) # Pythagoras
return cProgram 1:A function that computes the length of hypotenuse
def length_of_hypotenuse(a, b):
# YOUR CODE HERE
raise NotImplementedError()
return cYou can check your code against a few cases listed in the test cell below.
# tests
assert np.isclose(length_of_hypotenuse(0, 0), 0)
assert np.isclose(length_of_hypotenuse(3, 4), 5)
assert np.isclose(length_of_hypotenuse(4, 7), 8.06225774829855)If you are curious about the hidden test...
The hidden test will look like the following but with a "truely" random random _seed_:
rng = np.random.default_rng(_seed_)
a, b = rng.random(2)
assert np.isclose(length_of_hypotenuse(a, b), (a**2 + b**2) ** (0.5))# hidden testsWe will use ipywidgets to let user interact with the calculator more easily as illustrated in Figure 1:
- After running the cell, move the sliders to change the values of
aandb. - Observer that the value of
cis updated immediately.
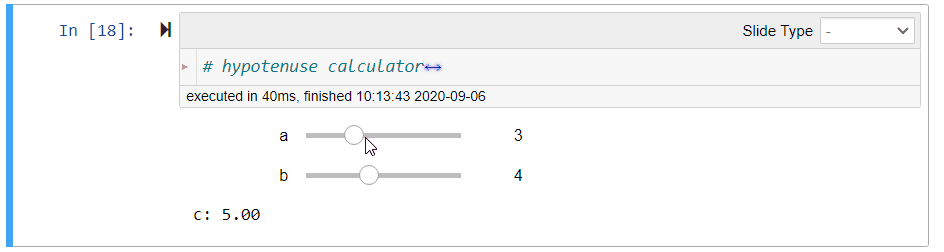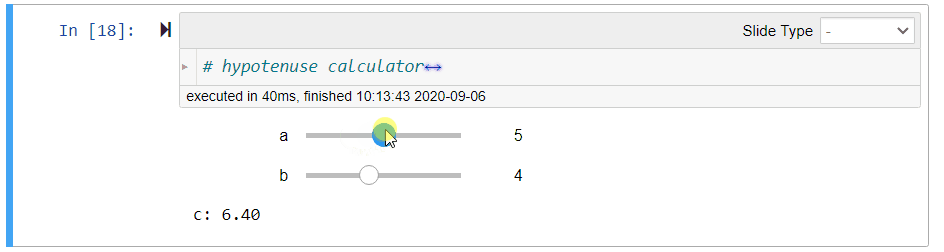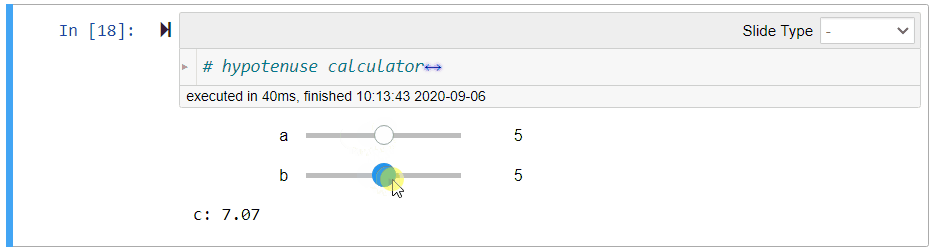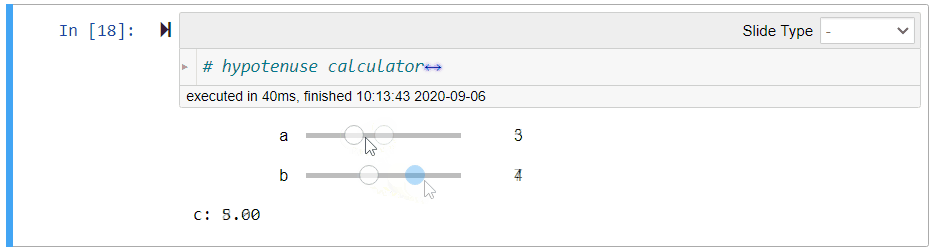
Figure 1:Illustration of the hypotenuse calculator
# hypotenuse calculator
@interact(a=(0, 10, 1), b=(0, 10, 1))
def calculate_hypotenuse(a=3, b=4):
print('c: {:.2f}'.format(length_of_hypotenuse(a, b)))The hypotenuse is printed up to 2 decimal places using the format specification {:.2f}.
Quadratic Equation¶
Graphical Calculator for Parabola¶
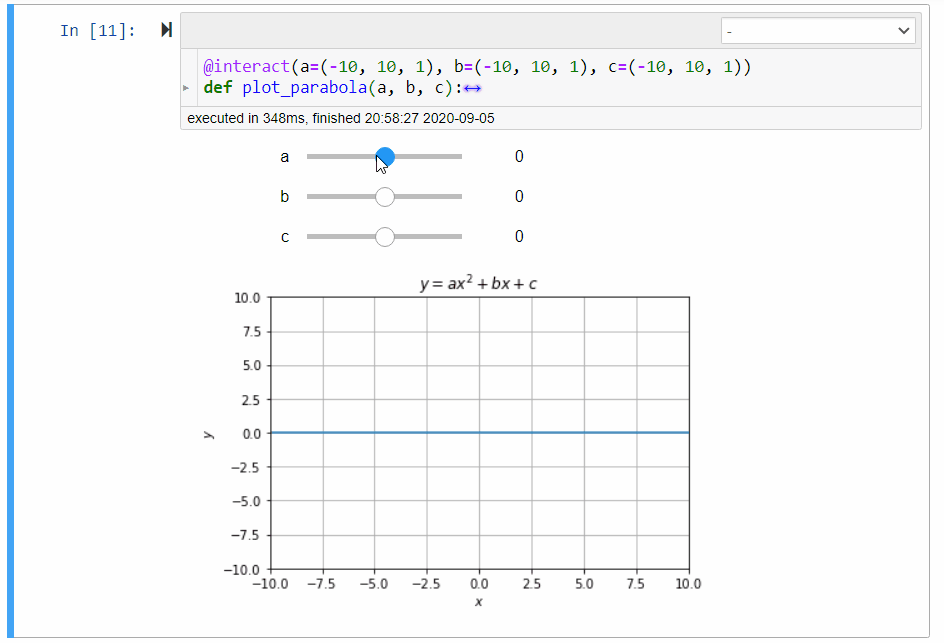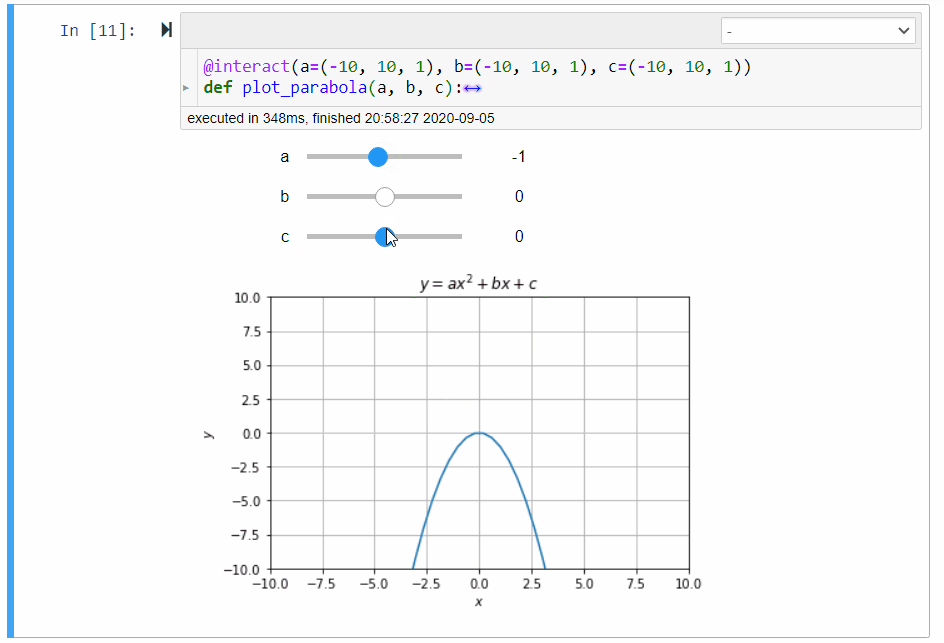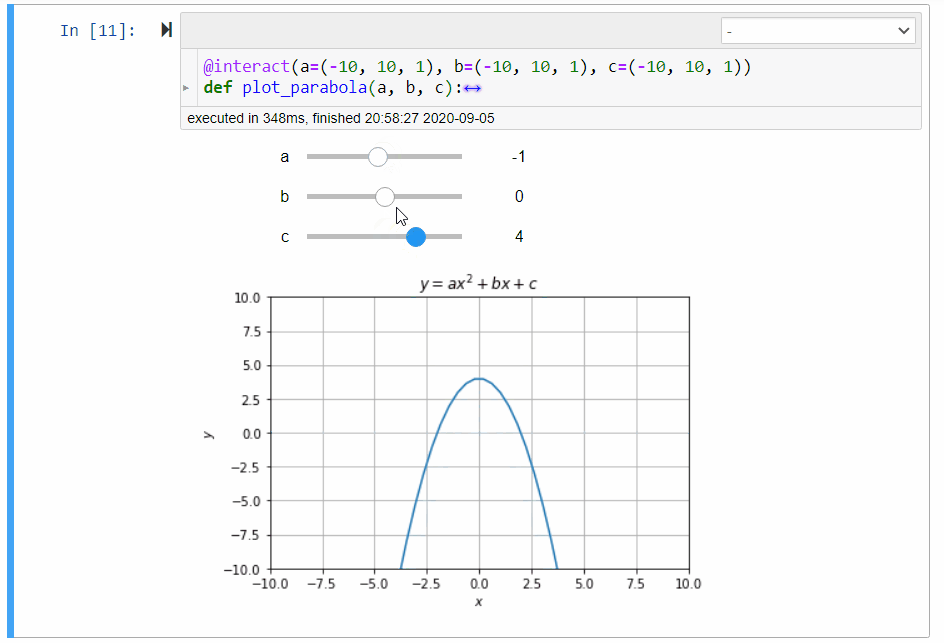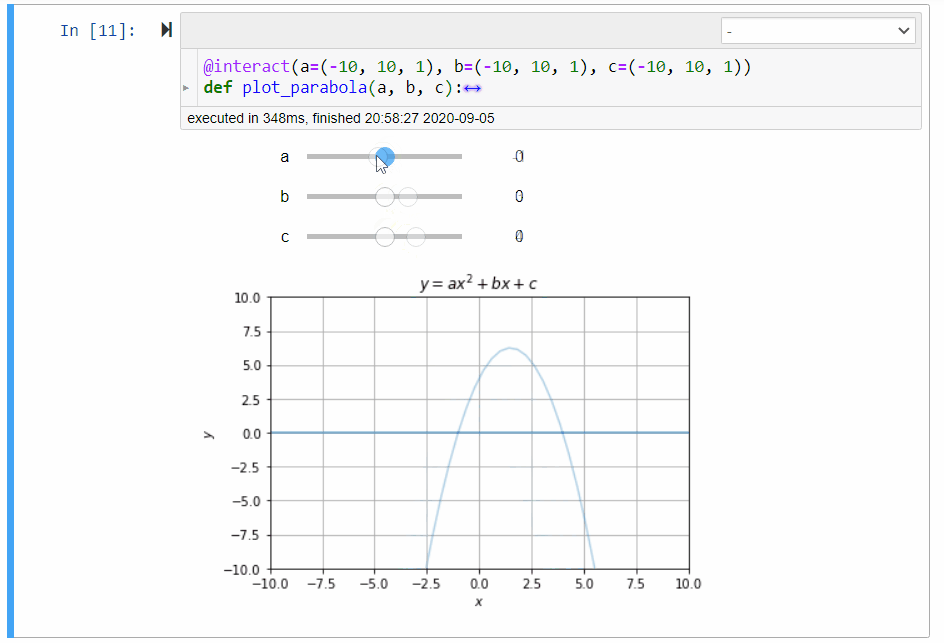
Figure 2:Illustration of the parabola calculator
The collection of points satisfying the following equation forms a parabola:
where , , and are real numbers called the coefficients.
The following plots the parabola with difference choices of coefficients.
jsxgraphs.parabolaGiven the variables x, a, b, and c store the -coordinate and the coefficients , , and respectively, assign y the corresponding -coordinate of the parabola (2).
def get_y(x, a, b, c):
# YOUR CODE HERE
raise NotImplementedError()
return yTo test your code:
# tests
assert np.isclose(get_y(0, 0, 0, 0), 0)
assert np.isclose(get_y(0, 1, 2, 1), 1)
assert np.isclose(get_y(0, 2, 1, 2), 2)
assert np.isclose(get_y(1.2, 2, 3, 4), 10.48)
assert np.isclose(get_y(2, 3.3, 4, 5), 26.2)
assert np.isclose(get_y(3, 4.4, 5, 6), 60.6)# hidden testsTo run the graphical calculator illustrate in Figure 2:
# graphical calculator for parabola
fig, ax = plt.subplots()
xmin, xmax, ymin, ymax, resolution = -10, 10, -10, 10, 50
x = np.linspace(xmin, xmax, resolution)
ax.set_title(r"$y=ax^2+bx+c$")
ax.set_xlabel(r"$x$")
ax.set_ylabel(r"$y$")
ax.set_xlim([xmin, xmax])
ax.set_ylim([ymin, ymax])
ax.grid()
(p,) = ax.plot(x, get_y(x, 0, 0, 0))
@interact(a=(-10, 10, 1), b=(-10, 10, 1), c=(-10, 10, 1))
def plot_parabola(a, b, c):
p.set_ydata(get_y(x, a, b, c))Quadratic Equation Solver¶
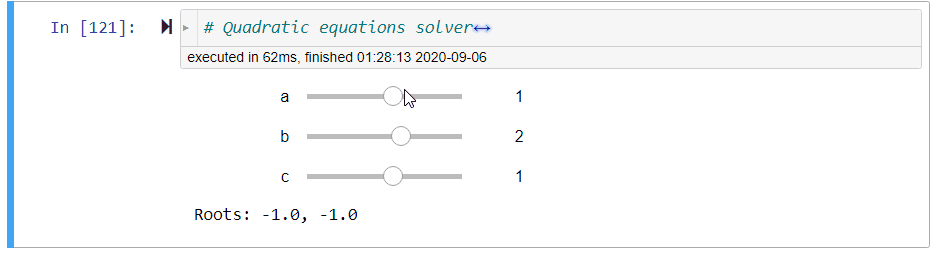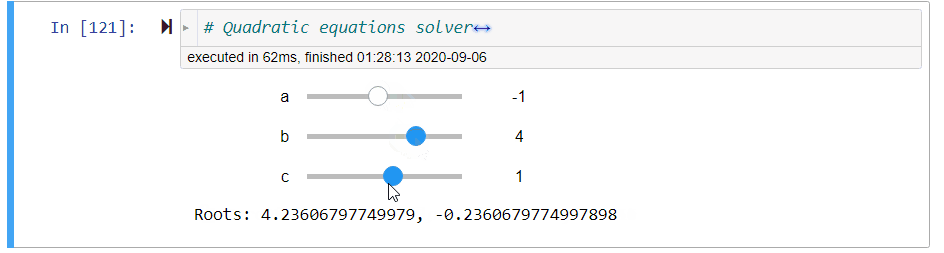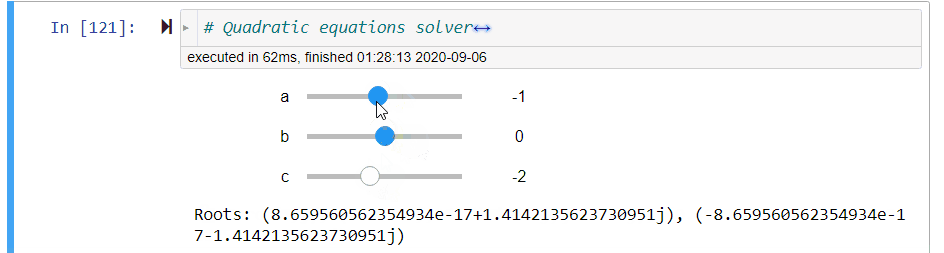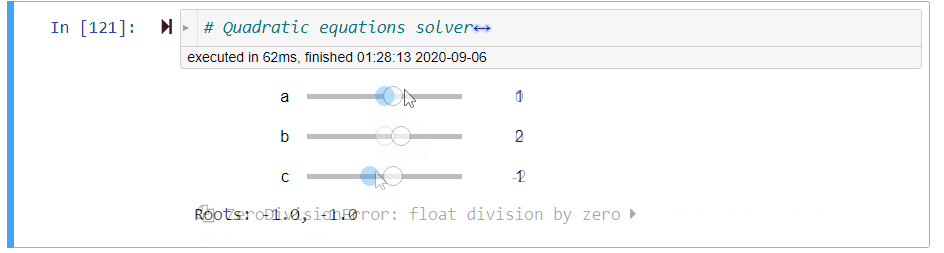
Figure 3:Illustration of the quadratic equation solver
Assign to root1 and root2 the values of the first and second roots in (4) above respectively.
Return the roots in the correct order and pay attention to the associativity of the arithmetic operators.
def get_roots(a, b, c):
# YOUR CODE HERE
raise NotImplementedError()
return root1, root2To test your code:
# tests
assert np.isclose(get_roots(1, 1, 0), (-1.0, 0.0)).all()
assert np.isclose(get_roots(1, 2, 1), (-1.0, -1.0)).all()
assert np.isclose(get_roots(2, 2, 1), (-0.5 - 0.5j, -0.5 + 0.5j)).all()# hidden testsTo run the calculator illustrated in Figure 3:
# quadratic equations solver
@interact(a=(-10,10,1),b=(-10,10,1),c=(-10,10,1))
def quadratic_equation_solver(a=1,b=2,c=1):
print('Roots: {}, {}'.format(*get_roots(a,b,c)))Number Conversion¶
Byte-to-Decimal Calculator¶
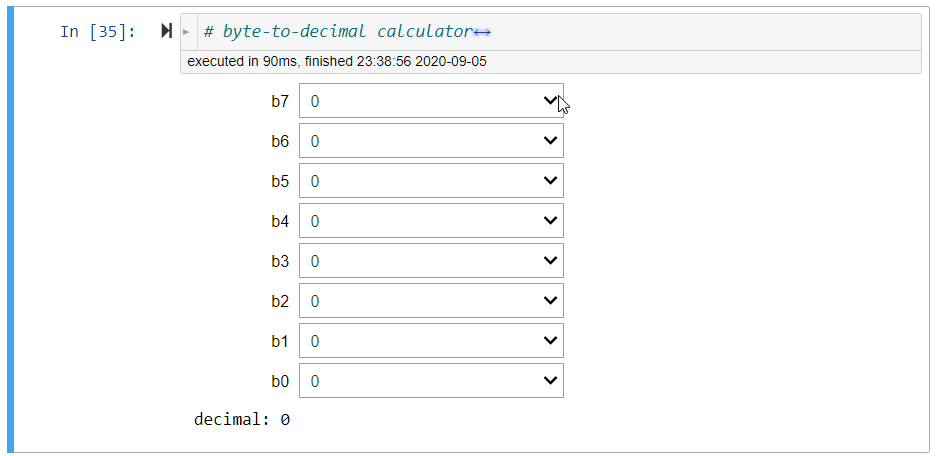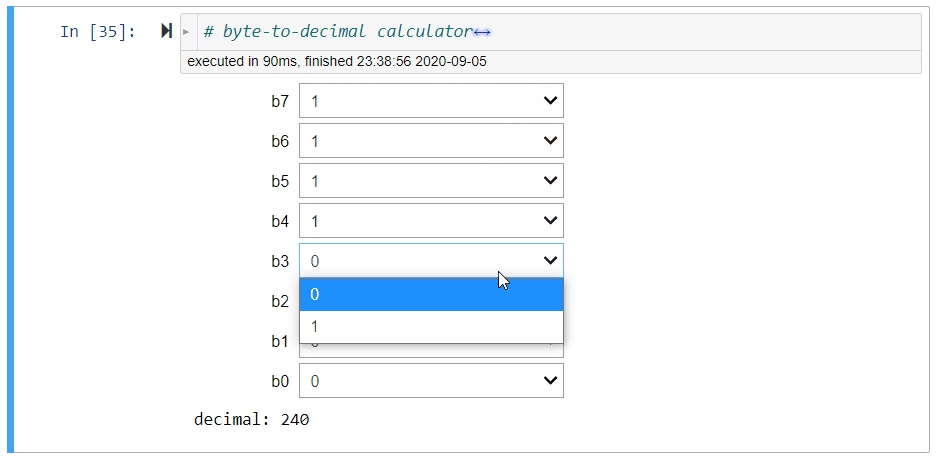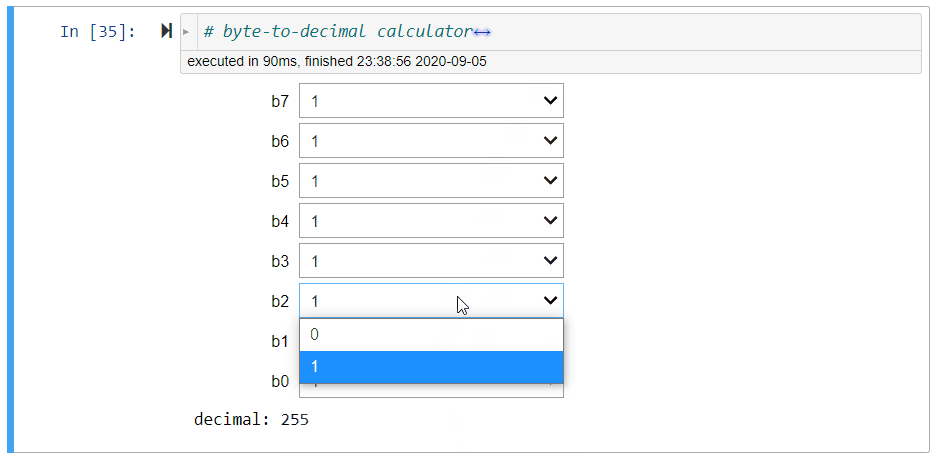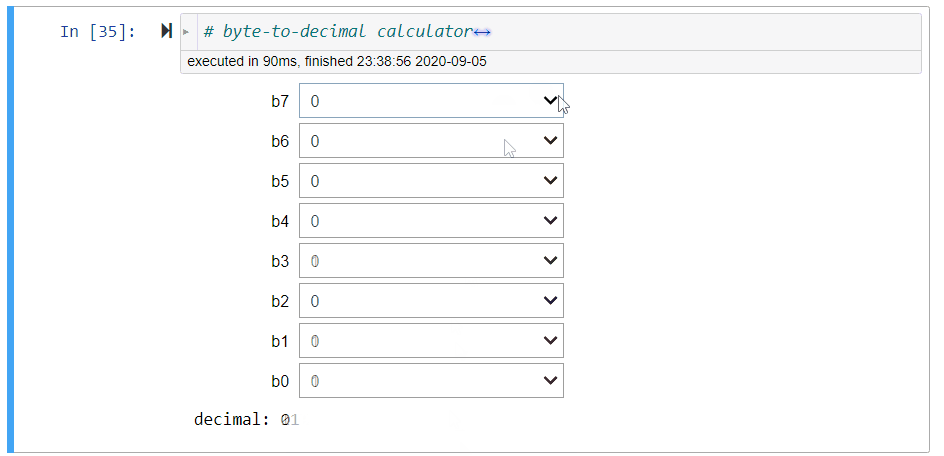
Figure 4:Illustration of the byte-to-decimal calculator
Denote a binary number stored as a byte (-bit) as
where concatenates 's together into a binary string.
The binary string can be converted to a decimal number by the formula
E.g., the binary string '11111111' is the largest integer represented by a byte:
Assign to decimal the integer value represented by the binary sequence b7,b6,b5,b4,b3,b2,b1,b0 of characters '0' or '1'.
def byte_to_decimal(b7, b6, b5, b4, b3, b2, b1, b0):
"""
Parameters
----------
b7, ..., b0: single characters either '0' or '1'.
"""
# YOUR CODE HERE
raise NotImplementedError()
return decimalTo test your code:
# tests
def test_byte_to_decimal(decimal, b7, b6, b5, b4, b3, b2, b1, b0):
decimal_ = byte_to_decimal(b7, b6, b5, b4, b3, b2, b1, b0)
assert decimal == decimal_ and isinstance(decimal_, int)
test_byte_to_decimal(38, "0", "0", "1", "0", "0", "1", "1", "0")
test_byte_to_decimal(20, "0", "0", "0", "1", "0", "1", "0", "0")
test_byte_to_decimal(22, "0", "0", "0", "1", "0", "1", "1", "0")
test_byte_to_decimal(146, '1', '0', '0', '1', '0', '0', '1', '0')
test_byte_to_decimal(128, '1', '0', '0', '0', '0', '0', '0', '0')
test_byte_to_decimal(71, '0', '1', '0', '0', '0', '1', '1', '1')# hidden testsTo run the calculator illustrate in Figure 4:
# byte-to-decimal calculator
bit = ['0', '1']
@interact(b7=bit, b6=bit, b5=bit, b4=bit, b3=bit, b2=bit, b1=bit, b0=bit)
def convert_byte_to_decimal(b7, b6, b5, b4, b3, b2, b1, b0):
print('decimal:', byte_to_decimal(b7, b6, b5, b4, b3, b2, b1, b0))Decimal-to-Byte Calculator¶

Figure 5:Illustration of the decimal-to-byte calculator
Assign to byte a string of 8 bits that represents the value of decimal, a non-negative decimal integer from to .
Use the operators // and %, but not the function int.
def decimal_to_byte(decimal):
# YOUR CODE HERE
raise NotImplementedError()
return byteTo test your code:
# tests
def test_decimal_to_byte(byte, decimal):
byte_ = decimal_to_byte(decimal)
assert byte == byte_ and isinstance(byte, str) and len(byte) == 8
test_decimal_to_byte("01100111", 103)
test_decimal_to_byte("00000011", 3)
test_decimal_to_byte("00011100", 28)
test_decimal_to_byte('11011111', 223)
test_decimal_to_byte('00000100', 4)
test_decimal_to_byte('10011001', 153)
def test_decimal_to_byte(byte,decimal):
byte_ = decimal_to_byte(decimal)
correct = byte == byte_ and isinstance(byte, str) and len(byte) == 8
if not correct:
print(
f'{decimal} should be represented as the byte {byte}, not {byte_}.'
)
assert correct
test_decimal_to_byte('01100111', 103)
test_decimal_to_byte('00000011', 3)
test_decimal_to_byte('00011100', 28)# hidden testsTo run the calculator illustrate in Figure 5:
# decimal-to-byte calculator
@interact(decimal=(0, 255, 1))
def convert_decimal_to_byte(decimal=0):
print("byte:", decimal_to_byte(decimal))Symbolic calculators¶
Can we do complicated arithmetics with python. What about Calculus?
Try SymPy Gamma or SymPy Beta.
- Take a look at the different panels to learn about the solution:
Steps,Plot, andDerivative. - Try different random examples.
How does SymPy Gamma work?
- SymPy Gamma is a web application running SymPy, which is a python library for symbolic computation.
- SymPy Beta is a fork of SymPy Gamma that can run totally in the browser.
How to use SymPy?
The following line in the initialization cell imports the library:
import sympy as spWe need to define a symbolic variable and assign it to a python variable.
x = sp.symbols("x")
xThe SymPy expression for is:
f = sp.tan(x)
fTo compute the integration:
g = sp.integrate(f)
gTo compute the derivative:
diff_g = sp.diff(g)
diff_gThe answer can be simplified as expected:
diff_g.simplify()To plot the functions:
p = sp.plot(f, g, (x, -2 * sp.pi / 5, 2 * sp.pi / 5), ylabel="y", legend=True)Using SymPy expressions
- assign to
xa SymPy variable named"x", - assign to
fthe expression in terms ofx, - assign to
gthe result of , and - optionally, plot
fandgfor .
Use sp.sqrt or **(sp.S(1)/2) for square root instead of **0.5. See SymPy gotchas.
# YOUR CODE HERE
raise NotImplementedError()The following test should plot your expression f in SymPy.
# tests
assert sp.simplify(f.subs(x, 0) - 1) == 0
assert sp.simplify(f.subs(x, sp.S(1)/2) - sp.sqrt(3)*2/3) == 0# hidden tests